分类： 未分类

做题的时候发现一个叫“搜集”的名词……
不知道是什么意思……
后来才在书上找到……
集合的概念：集合在某些场合又称为类、族或搜集。
【手动再见- -||】

并搜集和交搜集的概念：

简而言之，A的并搜集就是：A的所有子集里面包含的元素的并
A的交搜集就是：A的所有子集里面包含的元素的交

举个栗子~：
求A = {{Φ, 2}, {2}}的并搜集和交搜集：
先把A的子集都写出来：Φ、{{Φ, 2}}、{{2}}、{{Φ, 2}, {2}}
然后它有的所有元素是：{Φ, 2}、{2}
然后并搜集就是这两个元素的并：【这两个元素明显是两个集合嘛，所以就是求两个集合的并】——结果是{Φ, 2}
同理，交搜集就是求这两个元素的交：——结果是{2}

异步性是指进程以不可预知的速度向前推进。内存中的每个进程何时执行,何时暂停,以怎样的速度向前推进,每道程序总共需要多少时间才能完成等,都是不可预知的。
是程序并发执行时，程序之间的相互制约关系导致了并发程序这种“执行——暂停——执行”这种间断性的活动规律。

比如，当正在执行的进程提出某种资源请求时，如打印请求，而此时打印机正在为其他某进程打印，由于打印机属于临界资源，因此正在执行的进程必须等待，且放弃处理机，直到打印机空闲，并再次把处理机分配给该进程时，该进程方能继续执行。可见，由于资源等因素的限制，进程的执行通常都不是“一气呵成”，而是以“停停走走”的方式运行。

异步性就是描述进程这种以不可预知的速度走走停停、何时开始何时暂停何时结束不可预知的性质。

也就是说，如果传统意义上的程序没有在操作系统中为之配备进程控制块（PCB），没有用它来描述进程基本情况和活动过程，进而控制和管理进程，这样就会使程序在并发执行的时候失去其封闭性，也失去了可再现性。
但是，如果操作系统采用了进程同步机制，虽然程序具有异步性（走走停停、以不可预知的速度前进），但仍能保证进程并发执行的结果是可再现的。

所以，只要在操作系统中配置有完善的进程同步机制，且运行环境相同，作业经多次运行都会获得完全相同的结果。因此，异步运行方式是允许的。

偏序关系、全序关系都是公理集合论中的一种二元关系。
偏序集合：配备了偏序关系的集合。
全序集合：配备了全序关系的集合。

偏序：集合内只有部分元素之间在这个关系下是可以比较的。
比如：比如复数集中并不是所有的数都可以比较大小，那么“大小”就是复数集的一个偏序关系。

全序：集合内任何一对元素在在这个关系下都是相互可比较的。
比如：有限长度的序列按字典序是全序的。最常见的是单词在字典中是全序的。

偏序的定义：
设R是集合A上的一个二元关系，若R满足：
Ⅰ 自反性：对任意x∈A，有xRx；
Ⅱ 反对称性（即反对称关系）：对任意x,y∈A，若xRy，且yRx，则x=y；
Ⅲ 传递性：对任意x, y,z∈A，若xRy，且yRz，则xRz。
则称R为A上的偏序关系。

全序的定义：
设集合X上有一全序关系，如果我们把这种关系用 ≤ 表述，则下列陈述对于 X 中的所有 a, b 和 c 成立：
如果 a ≤ b 且 b ≤ a 则 a = b (反对称性)
如果 a ≤ b 且 b ≤ c 则 a ≤ c (传递性)
a ≤ b 或 b ≤ a (完全性)

注意：完全性本身也包括了自反性。
所以，全序关系必是偏序关系。

满射：对任意b，存在a满足f(a) = b。

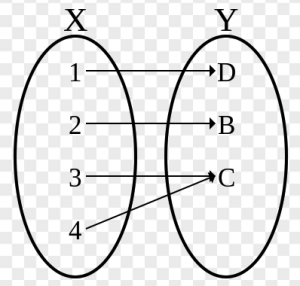
即：值域y是满的。每个y都有x对应。不存在某个y没有x对应的情况。

单射：(one-to-one function) 一对一函数。x不同则y不同。

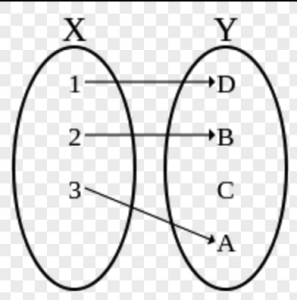
即：没有一个x对应两个y，也没有一个y有对应两个x。

双射：既是满射，也是单射。

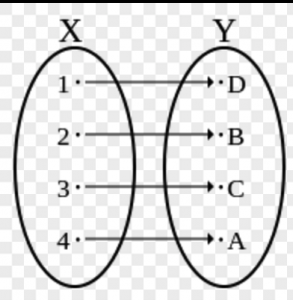
即：每个y都有x对应。而且都是一一对应。