







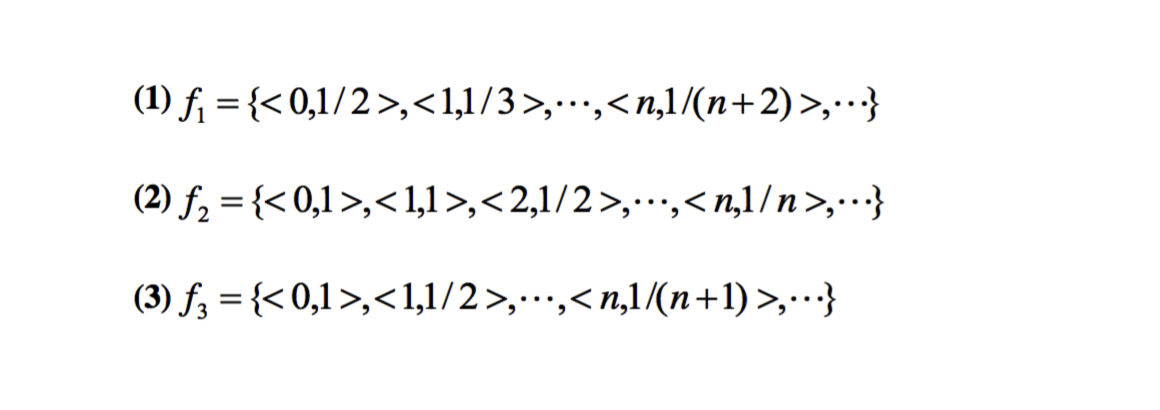
标签: 离散数学
【离散数学】最大元素、最小元素、极大元素、极小元素、上界、下界、最小上界(上确界)、最大下界(下确界)
设(A, ≤)是一偏序集合,B是A的子集。
最大元素、最小元素:
(1)元素b∈B是B的最大元素,如果对每一元素x∈B,x≤b
(2)元素b∈B是B的最小元素,如果对每一元素x∈B,b≤x
即:对于每一个元素,都能满足这样的偏序关系。
定理:如果B存在最大(最小)元素,那么它是唯一的。
例:如果B = {2, 3},偏序关系为“整除”,因为2和3互相不能整除,那么B没有最小元素和最大元素。
极大元素、极小元素:
(1)如果b∈B,且B中不存在元素x,使b≠x且b≤x,那么元素b∈B叫做B的极大元素。
(2)如果b∈B,且B中不存在元素x,使b≠x且x≤b,那么元素b∈B叫做B的极小元素。
即:对于极大元素,不存在元素在它偏序关系之上。对于极小元素,不存在元素在它偏序关系之下。
注意:B的最大(小)元素和极大(小)元素都必须是子集B的元素,而B的上界(下界)和最小上界(最大下界)可以是也可以不是B的元素。在定义中并没有保证这些元素的存在。在许多情况下他们是不存在的。
上界、下界:
(1)如果对每一b∈B,b≤a,那么元素a∈A叫做B的上界;
(2)如果对于如果对每一b∈B,a≤b,那么元素a∈A叫做B的上界;
上界、下界是A集合里的,可以存在很多个,也可以不存在
也就是说求上界的时候,对于每一个B里面的元素,都要和它上界们满足偏序关系,所以在集合B里面的不能有两个及以上,因为同事选择两个的话,就不满足B里面任何元素都要满足偏序关系了。
上确界、下确界:
(1)如果a是一上界并且对每一B的上界a’有a≤a’,那么元素a∈A叫做B的最小上界,记作lub;
(2)如果a是一下界并且对每一B的下界a’有a≤a’,那么元素a∈A叫做B的最大下界,记作glb
最大下界和最小上界可能存在也可能不存在,如果它们存在,则是唯一的。
如果最大值/最小值/上确界/下确界存在,那么一定是唯一的
求极大值/极小值的时候,因为只要是所有元素没有不满足的就可以,所以可以选择两个以上,其中可以有不和元素连线的。。
求上界/下界,因为是和最大最小值一样是所有的必须满足条件,所以所有元素都是要求有连线的,所以不可能存在两个及以上的元素在B集合里面。。
【离散数学】搜集、并搜集、交搜集、求A = {{Φ, 2}, {2}}的并搜集和交搜集
做题的时候发现一个叫“搜集”的名词……
不知道是什么意思……
后来才在书上找到……
集合的概念:集合在某些场合又称为类、族或搜集。
【手动再见- -||】
并搜集和交搜集的概念:

简而言之,A的并搜集就是:A的所有子集里面包含的元素的并
A的交搜集就是:A的所有子集里面包含的元素的交
举个栗子~:
求A = {{Φ, 2}, {2}}的并搜集和交搜集:
先把A的子集都写出来:Φ、{{Φ, 2}}、{{2}}、{{Φ, 2}, {2}}
然后它有的所有元素是:{Φ, 2}、{2}
然后并搜集就是这两个元素的并:【这两个元素明显是两个集合嘛,所以就是求两个集合的并】——结果是{Φ, 2}
同理,交搜集就是求这两个元素的交:——结果是{2}
【离散数学】单向连通和弱连通的区别

单向连通一定是弱连通的。
but,弱连通不一定是单向连通~~
举个栗子~
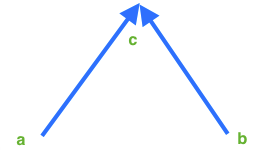
是弱连通~但不是单向连通~因为a和b结点,a不能到b,b不能到a~~
概念:
单向连通图
如果有向图中,对于任意节点v1和v2,至少存在从v1到v2和从v2到v1的路径中的一条,则原图为单向连通图。
即设G=<V,E>是有向图,如果u->v意味着图G至多包含一条从u到v的简单路径,则图G为单连通图。
强连通图、连通图、单向连通图三者之间的关系是,强连通图必然是单向连通的,单向连通图必然是弱连通图。
弱连通图
将有向图的所有的有向边替换为无向边,所得到的图称为原图的基图。如果一个有向图的基图是连通图,则有向图是弱连通图。
【离散数学】偏序关系与全序关系的区别、解释(偏序集合、全序集合)
偏序关系、全序关系都是公理集合论中的一种二元关系。
偏序集合:配备了偏序关系的集合。
全序集合:配备了全序关系的集合。
偏序:集合内只有部分元素之间在这个关系下是可以比较的。
比如:比如复数集中并不是所有的数都可以比较大小,那么“大小”就是复数集的一个偏序关系。
全序:集合内任何一对元素在在这个关系下都是相互可比较的。
比如:有限长度的序列按字典序是全序的。最常见的是单词在字典中是全序的。
偏序的定义:
设R是集合A上的一个二元关系,若R满足:
Ⅰ 自反性:对任意x∈A,有xRx;
Ⅱ 反对称性(即反对称关系):对任意x,y∈A,若xRy,且yRx,则x=y;
Ⅲ 传递性:对任意x, y,z∈A,若xRy,且yRz,则xRz。
则称R为A上的偏序关系。
全序的定义:
设集合X上有一全序关系,如果我们把这种关系用 ≤ 表述,则下列陈述对于 X 中的所有 a, b 和 c 成立:
如果 a ≤ b 且 b ≤ a 则 a = b (反对称性)
如果 a ≤ b 且 b ≤ c 则 a ≤ c (传递性)
a ≤ b 或 b ≤ a (完全性)
注意:完全性本身也包括了自反性。
所以,全序关系必是偏序关系。
【离散数学】单射、满射和双射的定义、区别
满射:对任意b,存在a满足f(a) = b。
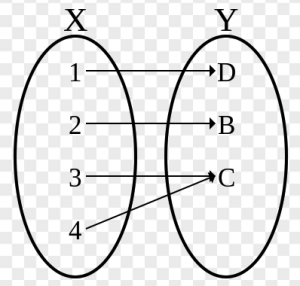
即:值域y是满的。每个y都有x对应。不存在某个y没有x对应的情况。
单射:(one-to-one function) 一对一函数。x不同则y不同。
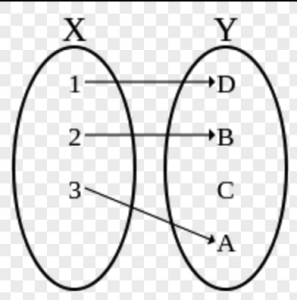
即:没有一个x对应两个y,也没有一个y有对应两个x。
双射:既是满射,也是单射。
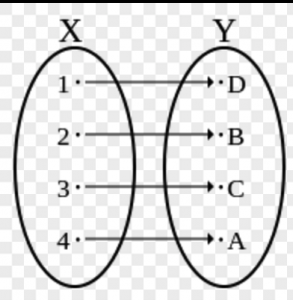
即:每个y都有x对应。而且都是一一对应。